Gametrees
Interaction is the essence of the computer game. Meaningful interaction requires that the computer respond to the actions of the player in a meaningful way. Since the player’s actions are expressions of his decision-making, we can characterize the player’s movement through the game as a series of branch points forming a path through a tree of possible actions:
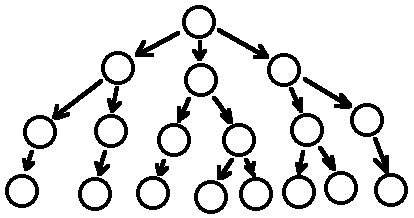
I have previously called this a "storynet"; for this article I shall call it a "gametree". Compare this structure with that of a story:
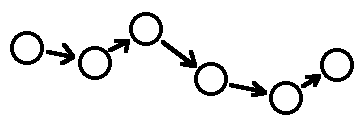
We note that the story’s structure is linear, a notion borne out by the often geometric terminology of storymaking. We speak of storylines or plotlines, a twist in the storyline, or the story taking an unexpected turn. A game’s structure is more complex. Note further that a single playing of a game constitutes a traversal of the gametree and is structurally identical to a story:
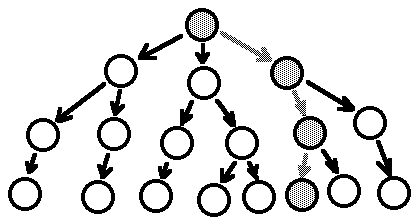
Thus, a game might be called a metastory, or perhaps a story-generator. The number of stories it can generate depends on the bushiness of the tree structure. A scrawny tree structure can generate only a few distinct stories, and the resultant game can therefore provide only a few decent replays. A thick, bushy tree provides a huge array of interesting choices to the player and can generate an abundance of stories and many happy replays.
The goal of the designer, then, must be to create the largest and bushiest possible tree structure. How can this be achieved?
Hard Wiring
The first approach is to directly specify each of the nodes in the tree. This hardwired approach to game design suffers from a profound limitation: the designer can never create enough nodes. Let’s walk through the numbers.
Suppose that you create a tree structure with 1,000 hard-wired nodes. Each node specifies the situation in which the player finds himself, the graphics, animation, and sound associated with that situation, the options available to the player, and the consequences of each option expressed in terms of the identities of the situations into which each chosen option would propel the player. For purposes of simplicity, let us assume first that each node provides the player with exactly three options, and that there is no degeneracy in the tree structure, that is, no two options anywhere in the tree lead to the same consequent node. Given these assumptions, then the tree will have a total of six layers in it, with 729 final outcomes. Thus, the game will be only six turns long, and there are only 729 possible outcomes. Compare this with Tic-Tac-Toe, a game capable of generating about 500 possible outcomes. Chess can generate something like 10**126 possible outcomes, if my memory serves me. Obviously the hardwired approach does not produce rich games.
Maze plus state variables
There is another way to create a large and bushy gametree. First, we create a maze through which the player moves. The player’s spatial path through the maze then corresponds to his gamepath through the gametree.
This scheme creates a gigantic tree from a small maze. The number of distinct paths through a maze increases very rapidly with the size of the maze. There is, however, a fatal flaw in the pure maze scheme: the gametree is degenerate. That is, a single junction in the maze may correspond to thousands of nodes in the gametree, but the nodes are indistinguishable. The player coming to that junction for the tenth time faces exactly the same choices that he faced on the first pass through the junction. If we collapse all the identical portions of the gametree together, it shrinks to microscopic proportions, with just one node for each junction.
There is salvation for the scheme: we endow the maze with state variables that the player acts on as he travels. The state variables might be changeable by the simple act of travel, or perhaps by more complex behavior on the player’s part, or perhaps by factors outside of the player’s control. If these state variables change often enough, then each time the player comes to a junction, the state variables will have taken new values, and the node in the gametree corresponding to this junction will be distinguishable from all the other nodes corresponding to this junction.
Examples: Pac-Man and Zork
Pac-Man uses this technique. There is a simple maze with a few dozen nodes. There are four groups of state variables: the status (eaten or uneaten) of the regular food-dots; the position of the four ghosts; the status (used or unused) of the power pills; and the state of the player (empowered or not empowered). These state variables insure that the player’s options at a given location take on new meanings each time he encounters that location. Thus, suppose that our hero comes to a junction and finds Blinky the ghost just to his left. At this junction, under these circumstances (state variables), the player would want to move to the right. Suppose, however, that at a later time he returns to this junction and finds Pinky the ghost just below him. Under these circumstances he would want to move up -- unless, of course, the player is empowered, in which case, he would want to move down. A single maze junction can generate zillions of gametree nodes, all because of the state variables.
Zork uses exactly the same design strategy. It too has a maze through which the player moves. The maze by itself would be uninteresting, but the state variables associated with the maze enable it to generate a truly interesting gametree. When the player enters a given room in Zork, the range of possibilities available to him depends on the state variables, most of which are simple Boolean variables. If the player has set the appropriate state variable TRUE (by reading the book, breaking the window, lighting the candle, or whatever), then the room will offer him options otherwise unavailable.
There is an interesting weakness in the traditional text adventure exemplified by Zork. Only a very few of the state variables will be meaningful in any particular room. Having the book in hand may save your life in one room, but will have no effect whatever in most of the others. Thus, the number of distinct nodes in the gametree associated with these rooms is limited, and the gametree is correspondingly emaciated. This suggests that game designers should take care that many of the state variables be significant at each juncture in the game.
Refutatio
One could argue that the bushiness of the gametree is derived only from the state variables, and that the maze is therefore unnecessary. I will not defend the claim that mazes are a necessary component of all or even most games. I will, however, argue that the maze in games of such architectures does serve a useful purpose. To wit, a maze provides a simple way to express a large number of state variables. One could, after all, declare some random collection of, say, a thousand bits to represent the state variables for a game. These 128 bytes could take 10**300 different states, a rich enough gametree for most players. Mathematically, then, a small amount of effort put into the state variables could generate a huge gametree.
The mathematical richness of this scheme is meaningless if it cannot be communicated to the player, and indeed no player will tolerate a screen packed with a thousand 1s and 0s, with no apparent relationships between them. The perfect example of this point is the flight simulator, capable of communicating a large number of state variables (airspeed, altitude, pitch, yaw, roll, and the first time derivatives of these) in a direct sensory format.
A maze provides this service in a very simple-minded fashion. A maze is a device for structuring spatial movement. It reduces the infinite number of possible movements available to a player on an open plane to a handful of options. This simplification clarifies the player’s options and makes the game easier to play, even as it gives visual form to the state variables.
