Here’s how we determine the motion of the streamer relative to the earth. We start with some spherical trigonometry:
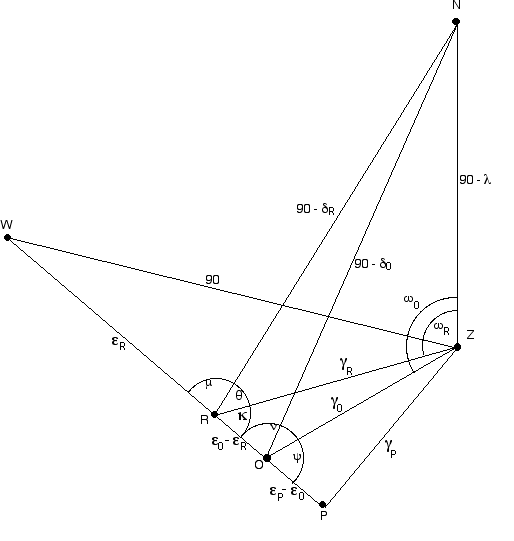
Figure 1: a portion of the celestial sphere
Definitions:
N: North celestial pole
Z: Zenith
O: direction of earth’s orbital vector
R: radiant of Leonid shower
The two points O and R define an arc.
W is the point where that arc intersects the horizon
P is the point on that arc closest to the zenith
λ is the latitude of the observer
γ is the zenith distance (90 - the altitude)
ε is the distance along the arc O - R, starting from W
α is the right ascension
δ is declination
ω is azimuth
μ ν κ ψ θ are the various angles shown
So here we go. Rather than present the formulae in standard mathematical format, which is a major pain to edit, I will simply paste in my C++ code. You may need to widen your window to see this clearly:
GammaR = acosf(sinf(Latitude) * sinf(DeltaR) + cosf(Latitude) * cosf(DeltaR) * cosf(AlphaR - SidTime));
OmegaR = acosf((sinf(DeltaR) - sinf(Latitude) * cosf(GammaR)) / (cosf(Latitude) * sinf(GammaR)));
GammaO = acosf(sinf(Latitude) * sinf(DeltaO) + cosf(Latitude) * cosf(DeltaO) * cosf(SidTime - AlphaO));
OmegaO = acosf((sinf(DeltaO) - sinf(Latitude) * cosf(GammaO)) / (cosf(Latitude) * sinf(GammaO)));
Theta = asinf(cosf(Latitude) * sinf(AlphaR - SidTime) / sinf(GammaR));
EpsO_EpsR = acosf(sinf(DeltaR) * sinf(DeltaO) + cosf(DeltaR) * cosf(DeltaO) * cosf(AlphaR - AlphaO));
Kappa = asinf(sinf(GammaO) * sinf(OmegaO - OmegaR) / sinf(EpsO_EpsR));
Mu = Pi - Kappa - Theta;
Nu = asinf(sinf(GammaR) * sinf(OmegaO - OmegaR) / sinf(EpsO_EpsR));
Psi = Pi - Nu;
GammaP = asinf(sinf(Psi) * sinf(GammaO));
EpsP_EpsO = acosf(cosf(GammaO)/cosf(GammaP));
EpsP = Pi / 2.0;
EpsO = EpsP - EpsP_EpsO;
EpsR = EpsO - EpsO_EpsR;
OmegaP = OmegaO - asinf(sinf(EpsP_EpsO) * sinf(Psi) / sinf(GammaP));
Now we shift to an elevation view, tilted by GammaP degrees, of the ground, atmosphere, and meteor:
Figure 2: from the side, but tilted at angle GammaP
I: projected impact point of meteor
M: first point of of appearance of the meteor in the atmosphere
h: termination height
ve: heliocentric velocity of earth
S: first point of of appearance in the atmosphere of a second meteor at time t
Beta = EpsR - EpsO;
d = Ve * t * sinf(Beta) / sinf(EpsR);
And now we return to a plan view; we’re looking down from space onto the atmosphere.
I: same as in Figure 2 (the projected point of impact of the first meteor)
B: the position of the observer
P’: the point where the line from the observer to point P in the celestial sphere intersects the top of the atmosphere
S’: the point where the line from the observer to point S in Figure 2 intersects the top of the atmosphere
R’: the point where the line from the observer to the radiant in the celestial sphere intersects the top of the atmosphere
ω: azimuth

Figure 3: plan view
OmegaL = 90 + OmegaP;
Phi = OmegaM - OmegaL;
n = h * tanf(GammaM);
m = powf(n * n + d * d - 2.0 * n * d * cosf(Phi), 0.5);
GammaS = atanf(m / h);
if (OmegaM > OmegaL)
OmegaS = OmegaM + asinf(d * sinf(Phi) / m);
else
OmegaS = OmegaM - asinf(d * sinf(Phi) / m);
This gives us GammaS and OmegaS, the position in the sky where the second meteor should appear.
